УДК 681

УДК 681.3.02

Принципы разработки межплатформенного класса cBigNumber для реализации
арифметических операций над целыми числами неограниченной разрядности

Р.Н.Шакиров

Институт машиноведения УрО РАН

raul@imach.uran.ru

Класс cBigNumber реализует все штатные целочисленные операции языка С++ для чисел неограниченной разрядности. Дополнительные функции - возведение в степень по модулю, квадратный корень и проверка на простоту по методу Миллера. Класс обладает встроенными средствами контроля и компенсации ошибок, оптимизирован для чисел размером от 500 до 20,000 двоичных разрядов. Испытания проводились для чисел размером до 12,000,000 двоичных разрядов.

Ключевые слова: C++, целочисленная арифметика, неограниченная разрядность, контроль ошибок, компенсация ошибок, метод Миллера.

1. Основные требования к классу неограниченных целых чисел

Поскольку операции над неограниченными целыми числами не предусматриваются в качестве штатных в распространенных языках программирования, то нами была поставлена задача разработки класса неограниченных целых чисел (далее просто класса), который в максимальной степени отвечает требованиям корректности, переносимости и универсальности. Наряду с выполнением указанных основных требований, класс должен обеспечивать оптимальную производительность для чисел небольшой разрядности. От аналогов класс должен отличаться предельной простотой использования, для чего он, прежде всего, не должен быть привязан к конкретной аппаратуре, операционной системе и транслятору. Остановимся на указанных требованиях более подробно.

1.1. Можно ли разработать корректно работающий класс неограниченных целых чисел?

Первое требование к классу – это корректное выполнение операций в соответствии с правилами целочисленной арифметики. Данное требование представляется совершенно тривиальным, однако именно его труднее всего выполнить – принимая во внимание логическую сложность многих целочисленных алгоритмов. В качестве примеров из прошлого можно привести один из первых отечественных вычислителей, который зависал при попытке умножить 0 на 0, а также известную ошибку деления в процессоре Pentium. Отметим, что в обоих случаях речь идет об устройствах с фиксированной разрядностью, что само по себе значительно упрощает задачу.

В качестве примера сложностей, которые возникают при неограниченной разрядности, представим себе метод класса, который делит целые числа в двоичном дополнительном коде. Пусть даны делимое и делитель, надо распределить оперативную память под частное и выполнить операцию. Поскольку речь идет о целых числах, то частное по модулю не больше делимого, поэтому распределяем для него тот же объем памяти, что и для делимого. Ошибка, которую мы допустили, заключается в предположении о том, что равные по модулю числа занимают одинаковый объем памяти. Это неверно – число -2147483648 в двоичном дополнительном коде занимает одно 32-разрядное слово, а число +2147483648 – два слова. Поэтому при делении -2147483648 на -1 для результата надо распределить не одно, а два 32-разрядных слова (рис.1).

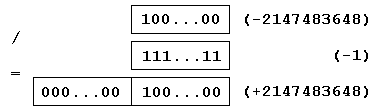
Рис 1. Пример деления (старшие слова и биты слева)

Оценим вероятность того, что допущенная нами логическая ошибка будет обнаружена при тестировании метода на сгенерированных случайным образом парах чисел, каждое из которых помещается в одно слово. Вероятность получить указанную в примере пару чисел равна (1/2³²)² = 1/2⁶⁴. Предположим, что мы проверяем миллиард пар в секунду (при современном состоянии техники для этого потребуется кластер из нескольких тысяч компьютеров, т.к. даже полностью аппаратное деление занимает несколько десятков машинных тактов, а мы будем проводить деление более медленным программным способом). Тогда математическое ожидание времени обнаружения ошибки будет 2⁶⁴/ (2 * 10⁹ * 3600 * 24 * 365.25) » 292 года. Это оптимистическая оценка, потому что на практике ошибки распределения памяти не обязательно проявляют себя легко обнаруживаемым способом.

Приведенный пример показывает невозможность корректной реализации арифметических операций по традиционной схеме программирование-отладка-тестирование. Конечно, можно утешить себя помышлением о том, что чем больше мы тестируем класс, тем меньше ошибок в нем остается. А при интенсивном тестировании и исправлении класса в течение нескольких сотен лет количество ошибок в нем будет асимптотически стремиться к нулю. Вопрос только в том, можно ли применять «асимптотически корректный» класс там, где требуется математическая корректность.

Положение можно несколько улучшить путем эмпирического анализа типичных программистских ошибок, после чего их можно исключить путем встраивания в программу соответствующих средств контроля и компенсации - это тот путь, который принят в данной работе. Для определенных классов ошибок можно написать специализированные тесты, которые будут выполняться за приемлемое время. Но эти меры не дают полное решение проблемы, потому что полный перечень допускаемых нами логических ошибок заранее неизвестен.

В противовес традиционному подходу теоретики программирования предлагают создавать корректные программы с применением аппарата математической логики [1, 2]. Для написания программы автор должен доказать теорему о ее корректности, при этом исполняемый код порождается транслятором только после того, как он (транслятор, а не человек) проверит доказательство. Применение данной теории к существующим программам пока затруднено из-за сложности их внутренней логики, которая плохо поддается проверке формальными методами.

1.2. Может ли класс неограниченных чисел работать на различных трансляторах?

Казалось бы, что проблема переносимости не должна существовать в такой хорошо изученной области, как математические вычисления. Для этого существуют стандартизированные языки программирования, а также инструменты для верификации программ на предмет переносимости. Но нет – самый известный и разработанный пакет для работы с большими числами – GMP принципиально ориентирован на UNIX-платформы и MacOS, причем даже при таком существенном ограничении разработчики жалуются на то, что они с 1996 года нашли около 100 ошибок, связанных с применением различных трансляций: «We are seeing ever increasing problems with mis-compilations of the GMP code... Thus far, we've found on-the-order-of 100 compiler bugs.» [3]. Вопросы использования GMP на платформе Windows освещаются на сайте [4].

Фактор трансляции еще более усложняет вопрос о корректности работы класса. Для решения этой проблемы класс должен сопровождаться тестами, позволяющими выявлять ошибки трансляции, при этом сами тесты должны выполняться за приемлемое время.

1.3. Универсальность и производительность

Требование универсальности состоит в том, что класс должен поддерживать все арифметические операции базового языка программирования, а также такие важные дополнительные операции, как возведение в степень по модулю (binary exponentiation), извлечение корней и некоторые другие. Поддержка полного набора операций существенна с точки зрения оптимизации. К примеру, трансляторы заменяют операции умножения и деления на константы 2^kоперациями сдвига. Для неограниченных чисел такую оптимизацию можно будет провести вручную, если класс поддерживает операции сдвига. Кроме того, универсальность класса облегчает перенос программ, написанный для арифметики с фиксированной разрядностью. Желательно, чтобы перевод таких программ на арифметику без ограничения разрядности выполнялся путем простой замены деклараций.

Что же касается вопроса о достижении высокой производительности, то его имеет смысл ставить в том случае, если класс работает корректно - иначе получится соревнование на скорость получения неверного результата. Поэтому мы выбираем алгоритмы исходя из принципа простоты реализации, а для повышения производительности проводим оптимизацию программного кода.

2. Концепция класса cBigNumber

Цель разработки класса состоит в такой реализации базовых арифметических операций над неограниченными целыми числами, которая уменьшает вероятность арифметических ошибок, а в перспективе – гарантирует их отсутствие за счет применения формальных методов верификации. Поэтому на данном этапе работы отрабатываются технологические решения, направленные на максимальное упрощение логики работы класса.

Безошибочный класс создается для того, чтобы создавать на его основе безошибочные программы. Поэтому концепция предусматривает не только перспективу внутренней верификации класса, но и возможность формальной верификации использующей класс прикладной программы.

2.1. Инкапсуляция данных и проверка соблюдения спецификации

Возможность верификации прикладной программы закладывается при разработке спецификации класса. Для этого открытая часть класса содержит конструкторы неограниченных целых чисел и методы для выполнения арифметических операций. Операции записываются в стандартной арифметической нотации. Внутренние структуры данных размещаются в закрытой части класса, там же выполняется распределение памяти под неограниченные числа. Поскольку прикладной программист не занимается распределением памяти, он не сможет совершать технические ошибки, подобные описанной в разделе 1. При выполнении операций не надо соблюдать какие-либо явно или неявно подразумеваемые ограничения, например, эффекты переполнения разрядной сетки. Поэтому формальная верификация использующей класс прикладной программы становится проще, чем случае применения штатной арифметики с фиксированной разрядностью (интересно отметить, что во многих работах по формальной верификации возможность переполнения разрядной сетки игнорируется, т.е. предполагается применение неограниченных чисел).

Спецификация метода состоит из 1) статической части, проверяемой при компиляции, 2) предусловия с требованиями к операндам и 3) постусловия с ожидаемыми характеристиками результата. Предусловия и постусловия проверяются динамически, соответственно в начале работы метода и по его завершению. В качестве примера предусловия можно привести проверку деления на 0, а в постусловии обычно проверяется знак результата, т.к. практика показывает эффективность этого метода выявления внутренних ошибок (полная проверка постусловия по методу выполнения обратной операции не проводится). Аналогичная динамическая проверка проводится во всех основных внутренних методах и функциях класса для целей внутренней диагностики. Методы и функции класса, работающие с внутренним представлением числа, проверяют его целостность.

2.2. Распределение памяти со страховкой

Для распределения памяти в закрытой части класса задействованы разработанные нами шаблоны динамических массивов. Шаблоны обеспечивают два режима распределения памяти – автоматический для массивов неограниченного размера [5] и ручной со страховкой, когда программист задает требуемые размеры массива, а программа в процессе выполнения автоматически отслеживает ошибки выхода индекса за границу массива [6]. Применяя неограниченные массивы, можно написать формально корректный код, не учитывающий фактор ограниченности машинных ресурсов. Поэтому нами применяется ручное распределение памяти. В этом случае возможны ошибки распределения памяти, которые в определенных ситуациях будут приводить к ошибкам индексации. Но в отличие от ситуации раздела 1, потенциально неверный результат получен не будет, т.к. при ошибке индексации программа завершит работу с выдачей диагностики.

Для увеличения производительности предусмотрена возможность отключения контроля индексов, при этом шаблон автоматически добавляет к массиву дополнительный страховочный элемент. Данная страховка не равноценна контролю индексов, т.к. она компенсирует только один распространенный класс ошибок – обращение к элементу, следующему за последним в массиве (нетривиальный пример такой ошибки был рассмотрен в разделе 1). Поэтому гарантировать корректное отключение контроля индексов можно только при условии верификации распределения памяти.

Другой способ увеличить производительность состоит в уменьшении числа операций распределения памяти. Для этого задействованы штатные возможности шаблонов. Число распределений памяти под массив пропорционально логарифму его максимального размера. А при вычислении выражений память выделяется специальным шаблоном стека динамических массивов.

2.3. Применение «школьных» алгоритмов и машинно-независимого программирования

Поскольку класс оптимизируется на небольшую разрядность, то для выполнения операций применяются «школьные» алгоритмы со следующими усовершенствованиями:

1. «Блочный» вариант умножения, учитывающий ограниченность размеров процессорного кэша L1. Множимое делится на фрагменты с тем, чтобы повторные обращения к памяти группировались в пределах 8-килобайтного участка адресного пространства.

2. Умножение и деление с применением таблицы сдвигов соответственно, блока множимого и делителя.

3. Наличие комбинированных операций – умножения с накоплением, деления с остатком, извлечения целочисленного квадратного корня с остатком и возведения в степень по модулю.

Алгоритмы реализуются путем машинно-независимого программирования, т.к. применение для этой цели ассемблерных или машинных кодов усложняет верификацию, а также сужает область применения класса. Применение ассемблера допускается только в качестве дополнительной возможности - для увеличения производительности на вычислительном устройстве с конкретной системой команд.

3. Основные правила применения класса cBigNumber

Неограниченная целая переменная с нулевым начальным значением объявляется, как
cBigNumber bignum;

При объявлении переменной можно непосредственно присвоить короткое начальное значение типа long, а для присваивания длинного значения используется выражение с длинными числами или конструктор присваивания строки, который требует явного указания основания системы счисления в пределах от 2 до 16 или равного нулю. Нуль подразумевает десятичную, восьмеричную или шестнадцатеричную константу языка C, например:
cBigNumber bignum ("0x80000000", 0).

Класс реализует все возможности штатной арифметики языка C++ над знаковыми целыми числами, включая арифметические, логические и побитовые операции, операции сравнения, арифметические сдвиги, операторы потокового ввода-вывода << и >> со всеми целочисленными модификаторами, а также следующие дополнительные операции:
             cBigPow (a,b)                    Возведение a в степень b.
             cBigPowMod (a,b,mod) Возведение a в степень b по модулю mod.
             cBigSqrt (a)                       Целая часть квадратного корня.
      В качестве операндов могут применяться длинные числа и короткие числа типа long. Благодаря полноте реализации набора операций класс может применяться для перевода на длинные числа программ, ранее разработанных для короткой арифметики.

Ряд методов предназначен для оптимизации программ, в их числе:
             c.addmul (a,b)                   Прибавление к c результата умножения a на b
             c.setdivmod (a,b)              Деление с остатком (частное заносится в c, остаток в a).
             c.setsqrtrm (a)                  Квадратный корень с остатком (корень в c, остаток в а).

На основе методов класса написаны функции для определения простоты числа путем факторизации и по вероятностному методу Миллера [7].

4. Реализация класса cBigNumber

В соответствии с изложенной концепцией, прототип класса cBigNumber может быть реализован на любом языке программирования, поддерживающем инкапсуляцию данных, динамическое распределение памяти с контролем индексов и битовые операции над машинными словами, включая операции арифметического и логического побитового сдвига. Язык должен допускать переопределение стандартных операций и обеспечивать разработку программ, переносимых между компьютерами различной архитектуры. Исходя из этих требований, для реализации класса выбран язык C++ стандарта ISO/IEC 14882:1998(E), хотя возможно применение и многих других языков.

Для представления длинных целых чисел используется дополнительный двоичный код. Предполагается, что этот же код и для представления коротких машинных чисел с фиксированной разрядностью, что позволяет проводить комбинированные операции над длинными и короткими числами без преобразования формата.

Реализация класса инвариантна по отношению к разрядности машинного слова, т.к. для хранения длинного числа отводится переменное число слов. Конструктор класса по умолчанию создает объект с нулевым значением без выделения динамической памяти (это целесообразно при создании разреженных массивов из неограниченных чисел). Память отводится только при первом обращении к объекту, при этом резервируется определенное число машинных слов с учетом возможности дальнейшего увеличения числа. В среднем, резервируется 33% от минимально необходимого объема памяти; если этой памяти не хватит, то проводится повторное резервирование. При уменьшении числа вся высвобожденная память остается в резерве. Минимальное количество слов, отводимых под число – около 25. Независимо от размера резерва, арифметические операции проводятся только над значащей частью числа.

Собственно класс представляет собой объектную оболочку, выполняющую распределение памяти и операции ввода-вывода. Для выполнения арифметических операций класс обращается к служебным функциям, объявленным как extern «C», т.е. они при необходимости могут быть вызваны из программ на процедурно-ориентированном языке С (рис 2).

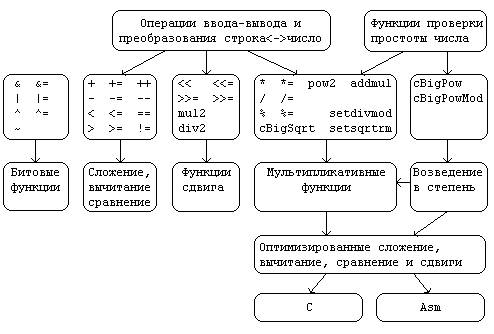
Рис. 2. Структура класса cBigNumber

Сложение, вычитание, операции сравнения, арифметические сдвиги и битовые операции реализованы машинно-независимым образом с применением логических масок. Операции оптимизированы по производительности для чисел размером не менее 200 бит, в этом случае они требуют от 1/5 до 1/2 машинного такта x586 на получение каждого двоичного разряда результата.

Мультипликативные операции (умножение, деление, возведение в степень и извлечение квадратного корня) реализованы с применением оптимизированных функций сложения, вычитания, сравнения и сдвига с накоплением. Оптимизированные функции имеют две реализации – машинно-независимую с масками и машинно-зависимую на аддитивных и сдвиговых операциях ассемблера x86, обе учитывающие архитектурные особенности суперскалярных процессоров. Ассемблерные функции тратят на получение одного слова результата от 2 до 3 тактов, машинно-независимые функции примерно в 3 раза медленнее. Умножение и возведение в степень оптимизированы для случая, когда размер хотя бы одного из операндов не менее 500 бит. Деление, модуль и возведение в степень по модулю оптимизированы для делителей размером от 500 бит до 1/32 от объема кэш-памяти компьютера: для кэша в 512 Кбайт оптимальный размер делителя будет до 120,000 бит. Оптимальный размер аргумента квадратного корня такой же, как для делителя.

При ассемблерной реализации число машинных тактов x586 для выполнения операции над числами оптимальной разрядности оценивается так:

· умножение и деление: mn/10, где m и n – разрядность операндов в битах;

· квадратный корень: n²/10, где n - разрядность числа;

· возведение в степень по модулю: 3n³/10, где n – разрядность делителя

Применение аддитивных операций, логических масок и сдвигов в качестве базовых оправдано еще и потому, что эти операции являются простейшими с точки зрения их реализации в аппаратуре и необходимыми для работы системного программного обеспечения. Если данные операции выполняются неправильно, например, в результате перегрева процессора, то это обстоятельство сопровождается неизбежным крахом системы. Потому можно рассчитывать на то, что аппаратура будет проводить указанные операции корректно. Единственное дополнительное условие состоит в том, что оперативная память компьютера должна обладать коррекцией ошибок (ECC) - чтобы там не происходило случайное искажение данных, сброшенных из кэша процессора.

В случае целочисленного умножения уверенность в корректной работе процессора слабее, а относительно деления ее и вовсе нет, поскольку операционная система эту операцию практически не использует - поэтому эпизодические ошибки при делении совершенно не мешают ей работать. Аналогичная картина наблюдается и при операциях с плавающей точкой, которые применяются во многих математических пакетах для умножения длинных чисел по методу FFT. На машинах архитектуры x86 эти операции выполняются в блоке FPU, который непринципиален для стабильной работы системы. Тест Prime95 показывает, что при «разгоне» или перегреве процессора блок FPU может выдавать ошибки притом, что операционная система работает без сбоев [8].

5. Тестирование класса cBigNumber

Как уже отмечалось в разделе 1, тестирование класса неограниченных чисел не позволяет гарантировать его корректность. Поэтому тестирование проводилось для того, чтобы отследить эффективность вспомогательных методов обеспечения корректности, которые обсуждаются в разделе 2. Предполагается, что при осуществлении формальной верификации класса необходимость в тестировании класса отпадет, т.к. все методы класса будут изначально работать без ошибок (при этом, однако, сохранится необходимость тестирования спецификации класса).

Для тестирования класса написана программа Arifexp, позволяющая проводить операции с длинными числами с проверкой результата по методу обратной операции. В программу встроен генератор примеров с равномерным распределением в пределах заданного минимального и максимального размера. С помощью генератора в начале 2003 года было проведено тестирование класса на более чем 20,000,000 случайных примерах с разрядностью от 1 до 12,000,000 бит.

По результатам тестирования в классе обнаружены и устранены следующие ошибки:

· 7 ошибок распределения памяти;

· 4 арифметические ошибки;

· 3 ошибки в операторах ввода-вывода и спецификации класса.

Все ошибки распределения памяти обнаружены встроенными средствами контроля индексов. При отключенном контроле индексов 1 ошибка приводила к аварийному завершению программы, 1 ошибка могла привести к выдаче неверного результата, остальные 5 ошибок были полностью скомпенсированы благодаря добавлению к массивам резервного элемента.

Арифметические ошибки обнаружены при делении и возведении в степень по модулю. В 1 случае сработал внутренний контроль постусловия (проверка знака), остальные 3 ошибки обнаружены при выполнении проверки по методу обратных операций.

Ошибки в операторах ввода-вывода и спецификации не могли приводить к выдаче неверного результата.

Таким образом, общее количество обнаруженных ошибок арифметического и потенциально арифметического характера равно 5, из них 2 обнаружены встроенными средствами контроля и 3 при проверке по методу обратной операции. Еще 5 потенциальных ошибок были скомпенсированы по методу резервного элемента. Общая эффективность встроенных в класс средств контроля и страховки составила (2 + 5) / (5 + 5) = 70%.

Заключение

Проведенный анализ показывает целесообразность формальной верификации программ, выполняющих арифметические вычисления с неограниченной разрядностью, т.к. этот метод позволяет гарантировать корректность результата. Альтернативой может служить ресурсоемкий контроль по методу обратной операции. Значительную часть ошибок можно предупредить по методу резервного элемента, а также путем контроля индексов и проверки постусловия операции, как это сделано в текущей версии класса cBigNumber. Программное обеспечение класса cBigNumber доступно для свободной загрузки на странице http://www.imach.uran.ru/cbignum.

Литература

1. Роберт Лоренс Бейбер. Программное обеспечение без ошибок. M.: Радио и связь, 1996. 176с.

2. В.А.Непомнящий, О.М.Рякин. Прикладные методы верификации программ. М.: Радио и связь, 1988. 256c.

3. The GNU MP Bignum Library: http://www.swox.com/gmp/

4. GMP Install Instruction for Windows Platform: http://www.cs.nyu.edu/exact/core/gmp/

5. Р.Н.Шакиров. Oценка эффективности динамических массивов с автоматической проверкой индекса // Новые информационные технологии в исследовании сложных структур: Докл. III Всеросс. конф. с межд. участием. Томск, 10-12 сентября 2002. С.383-388.

6. Р.Н.Шакиров. Шаблоны для организации контроля индексов в программах на языках С++ и С // IEEE AIS'03 CAD-2003: Труды конференций. Дивноморское, 3-10 сентября 2003. Т.2, С.191-207.

7. Miller strong probable prime test: http://www.utm.edu/research/primes/prove/prove2_3.html

8. Prime95 download page: http://www.mersenne.org/freesoft.htm